Book of the Week: Danyl Mclauchlan reviews a brilliant new biography of Friedrich Nietzsche, who declared, “I am not a man. I am dynamite!”
It ended in Turin, on January 3, 1889 when Friedrich Nietzsche shuffled into the Piazza Carlo Alberta. Nietzsche was a sad, solitary figure; he spent his days in Turin’s bookshops, reading but not buying the books, or roaming the streets dressed in worn, shabby clothes, his eyes – nearly blind but agonisingly sensitive to light – hidden behind thick green-lensed sunglasses, a green visor jutting out from his head like a beak. At the edge of the Piazza he created a disturbance: no one knows what happened: a story circulating after his death claims he saw a cart horse being flogged, ran to it, threw his arms around the animal to protect it then fell to the ground, weeping.
A crowd gathered. Two policemen led him back to his room; a tiny lodging above a newspaper shop, filled with manuscripts, volumes of philosophy, musical scores. He’d passed the last decade in places like this, drifting around Switzerland and northern Italy, living in poverty, borrowing money to self-publish his increasingly strange and blasphemous books, which nobody read.
He spent the next few days secluded, singing, raving, sending deranged letters to his family and friends signed “Caesar Nietzsche” or Dionysus or “The Crucified One”. At night his hosts heard him dancing. Peering through the keyhole they saw him capering, naked. He was 44-years-old with an enormous bristling moustache, powerfully built but emaciated from years of sickness. Last year he’d spent weeks confined to his bed, unable to sleep, existing in absolute darkness, devastated by migraines, hallucinating, vomiting blood, self-medicating with opium and chloral hydrate. Now he danced, chanting in Ancient Greek, performing the holy rites of Dionysus; rituals no one had celebrated for over two thousand years.
A friend arrived – Nietzsche had sent him a letter announcing he was about to take over the Reich – and escorted him back to Germany. He spent time in psychiatric clinics and was eventually released into the care of his mother, who had seen most of this before. Nietzsche’s father was a pastor and an acclaimed musician but in his mid-thirties he experienced a series of agonising headaches accompanied by fits of vomiting and blindness. He died at the age of 35; Nietzsche was five years old. Shortly afterwards his infant brother suffered a series of seizures and died of a stroke. Mental illness and suicide haunted the bloodline.
Nietzsche studied at the Pforta School, one of the most elite academies in Europe, where his teachers thought he was the most brilliant student the ancient classrooms had ever seen. At 24 he was the youngest professor ever appointed to a position at the University of Basel in 400 years. He taught philology, the study of classical languages. To his students he was more like a resident of the ancient world than the modern: he spoke about Pre-Socratic Greece as if he’d lived there. His closest friend was Richard Wagner, the most famous composer in the world: they walked together in the hills above Wagner’s estate discussing their plans for the rebirth of European culture.
And then it all unravelled. His books were mocked then – worse – ignored. His health deteriorated. His friendship with Wagner ended when Nietzsche saw that the composer was more interested in a new Germany than a new Europe, specifically a Germany made stronger by purifying it of Jews. His university paid him a sickness pension and Nietzsche began his years of wandering; roaming the Swiss alps in between bouts of sickness; hurrying to record his insights before the next attack came. His journey led him to uncover staggering new vistas of thought but ended in his childhood bedroom being tended to by his mother. When she died Nietzsche had regressed to a persistent vegetative state. He was given over to his brilliant but monstrous sister Elisabeth Forster-Nietzsche, who loomed over his life and cast a malevolent shadow over his legacy. He spoke little; never wrote. By the time of his death in 1900 he was one of the most famous philosophers in the world.

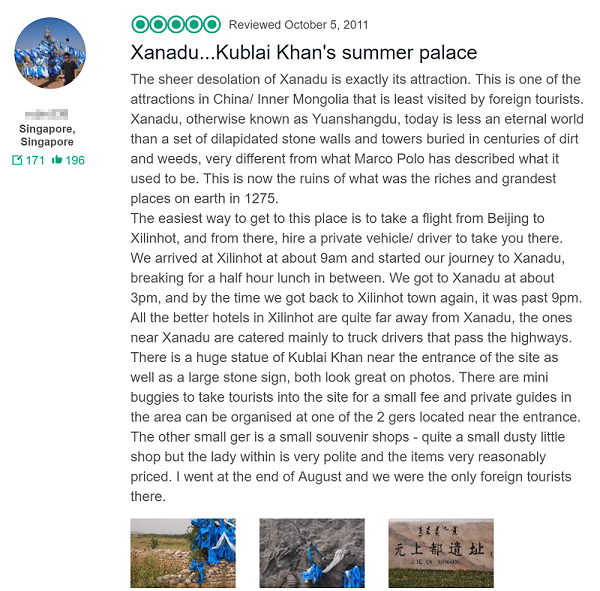
Sue Prideaux (Image: twitter @faberbooks)
There have been many studies of Nietzsche but I don’t expect to read a better biography than I Am Dynamite!: A Life of Nietzsche. Prideaux is not a philosopher; her previous works are about Strindberg and Munch, both of whom intersected with and were influenced by Nietzsche. And she’s a beautiful writer, often coming as close to a non-fiction novel as a biography can while remaining a work of historical scholarship. She’s especially good on the women in Nietzsche’s life, his cultural background, the relationship with Wagner and the labyrinth of artistic, philosophical, political and sexual mazes Nietzsche blundered into with amusing frequency. She knows just when to paraphrase and when to let Nietzsche – who is a great writer; one of the very few philosophers whose work functions as literature – speak for himself.
Most non-philosophers encounter Nietzsche through his aphorisms. “That which does not kill me makes me stronger.” “When you gaze into an abyss, the abyss gazes also into you.” Some people admire these sentiments so much they tattoo them onto their bodies in heavy gothic lettering – and you can admire them via a google image search – but what’s his overall message?
That’s difficult to say. Some of his books contain nothing but aphorisms, in no particular order or relation to each other. “I say in ten sentences what others say in a whole book – what others do not say in a book,” he boasted. Most philosophers promote their ideas via logical arguments; Nietzsche mocked this approach. Real insights are not achieved through mere reason, he scoffed. They are intuitive, inspired; all the neat arguments are just post-hoc justifications.
Many of his ideas seem contradictory. Other philosophers – normal philosophers of the 19th century – constructed systems: holistic, internally consistent logical frameworks that attempted to make sense of the world. Nietzsche is an explicitly anti-systemic philosopher. Systems constrain you. Systems and ideologies give people the illusion of understanding more than they think they do. “Conviction is a more dangerous enemy of truth than lies.” Instead he is “the philosopher of perhaps,” and he “philosophises with a hammer”. He wants to smash things apart, not put them together. Yet, despite all this internal contradiction and smashing of things there is a generally accepted core set of important ideas in Nietzsche’s work. They concern values, the death of God and nihilism.
One of the things that’s wrong with us as a species, Nietzsche argues, is our persistent belief that there is another, higher world; a spiritual world. This belief in fictional systems – religion, philosophy, astrology – devalues the real world where we live our actual lives. We’ve trapped ourselves in “an architecture of fear and awe, whose very foundation is the terror that death might lead to nothing more than oblivion”. These foolish superstitions are the basis for our civilisational values but they are life-denying values. Especially the values of Judaism and Christianity which are forms of “slave morality”.
The Jews and the Christians were slaves, first in Babylon then in Rome. They were powerless to impose their will upon the world but they lusted for power, as all living things do, so they were consumed with resentment against their masters. That is why both faiths are decadent inversions of true morality: they deny the reality of human nature and celebrate slavery and misery and suffering and victimhood.
*
When I was a teenager all I knew about Nietzsche is that he was the guy who said “God is dead,” and I assumed he was the first atheist philosopher, and that this must have been a big deal back in the day but was of little importance now. But philosophers had been making the case for atheism for centuries prior to Nietzsche: what he said about God is far more interesting.
God is dead, he tells us. But the statue of the dead God casts a vast and gruesome shadow over our civilisation. All of our values, our institutions, all of our assumptions about the world: our politics, our culture, our customs, our languages, or systems of thought – these are all inherited from earlier generations and they all have the assumption of the existence of God built into them. But all of those values are obsolete. Few believe in them but we behave as if we do. Thus we live in the age of “incomplete nihilism.” And when Nietzsche talks about religious values he isn’t talking about trivial prohibitions against stealing or committing adultery. He’s talking about the really big, deep stuff that we still take for granted. He’s talking, for example, about truth.
He argues that the idea of truth is a religious one based on the idea that there is a God who created the world and can directly apprehend it. But in the search for ‘truth’, philosophers and scientists revealed that this God does not exist. Instead of destroying religion, however, scientists have substituted themselves for priests and their discoveries for moral dogma.
But science is only an interpretation and arrangement of the world. “There are many kinds of eyes. Even the sphinx has eyes – and consequently there are many kinds of ‘truths,’ and consequently there is no truth.” Scientists claim to discover the truth, but if another more powerful theory about the world comes along they must abandon that truth for a new one – meaning it was never true at all. “There are no facts, only interpretations.” Words are but symbols for the relations of things to one another and to us; nowhere do they touch upon absolute truth.
Maybe you’re not interested in debates about science and truth. Maybe you’re more committed to kindness, or compassion or equality. Maybe you assume your investment in these values make you a good person and those who don’t share these values are flawed, or evil? But where do your beliefs come from? Why do you value them? Is the eagle evil for hunting its prey? Why then is the strong man evil for preying upon the weak? Are not the very ideas of ‘good’ and ‘evil’ religious values? Do they have any meaning in this post-religious world?
Most of us respond to these arguments with indignation and exasperation. Of course we should have compassion for each other! Of course everyone should be treated equally! And how can scientists make such accurate predictions if they aren’t discovering some form of truth about the nature of reality? How can it be true that there is no such thing as truth? But when you read Nietzsche’s mature works – On the Genealogy of Morals or Beyond Good and Evil – you quickly learn that Nietzsche is much, much smarter than you are, that he’s anticipated your objections and has frustratingly sophisticated arguments against them. Steven Pinker, in his book Enlightenment Now, an apology for liberal humanism and scientific rationalism, urges people to simply stop reading and teaching Nietzsche. He must be wrong, Pinker feels. It’s just very hard to say why.
Nietzsche is comfortable with your discomfort. If you want to go on believing in compassion and truth then he’s fine with that. Really. His books, he assures readers, are not for everyone. Truly they are not for the cowardly, the weak minded, the simple, bleating creatures of the herd who cannot think for themselves. His term for anyone who does not believe in God but still lives by religious values is ‘the Last Man’ (if you’re a woman Nietzsche gives even fewer shits about what you think: his mature philosophy is, Prideaux admits, deeply misogynistic). In one of his most famous passages he prophesies the safe, comfortable but meaningless lives of the world given over to the Last Men, passages that seem like a very accurate description of middle-class life in the liberal democracies of the twenty-first century.

Who are Nietzsche’s books for? They are for the superman. Man is the sick animal, “a hybrid between a plant and a ghost”, but he is also a rope across the abyss of nihilism: a bridge between the ape and the superman. Being human is a condition that can be overcome if we ignore those who offer extra-terrestrial hopes or the false promises of reason and materialism. The superman creates his own life-affirming values. He can scrub clean the shadow of the murdered God. “Become who you are”, Nietzsche urges his readers. Abandon religion and reason. “To give birth to a dancing star you must have chaos within.”
What on earth are we to make of . . . any of this? Anything we like!, was the giddy response of 20th century artists and intellectuals. Everyone borrowed from Nietzsche. Second-wave feminists took the idea of value creation in a direction he would never have imagined, would have barked at in fury; gender, they said, is a created value. Michel Foucault – arguably Nietzsche’s greatest disciple – went further. Sanity is a created value. So is sexuality. So is the very idea of ‘the human’. Everything we believe, everything we take for granted as ‘natural’ is a social construct – but they’re not religious constructs, Foucault declared: they’re manufactured by the institutions of the modern nation state. It was an idea that complimented the paranoid style in radical left-wing politics. After Foucault, schools, hospitals, universities and the media all became ‘vectors of power’, which manufactured values at the service of dominant ideologies – capitalism, patriarchy, white supremacy – while concealing themselves behind a neutral sign.
To religious conservatives Nietzsche’s warnings about the post-religious descent into nihilism are all the argument you need to return to traditional religion and the moral guidance of the church. Bolshevik intellectuals were delighted with the notion of the superman, which transformed into the ‘New Soviet Man’ who rose above bourgeois values. If you had to kill a lot of humans to give birth to the post-capitalist superhuman – well, those are the breaks. Ayn Rand’s novels are pure Nietzsche: The Fountainhead argues that creative artists exist outside any moral framework; in Atlas Shrugged the supermen have transformed into heroes of capitalism. Through Rand the notion that business leaders transcended conventional morality helped poison the corporate culture of the west, apotheosising itself in the Silicon Valley motto “Move fast and break things.” How else would a superman with no responsibilities to the mediocre cattle of humanity do business?
*
One you start looking for Nietzsche he’s everywhere. But his most notorious ideological association is with the Nazis: a connection that began with his family.
Nietzsche was a great hater of women, the great enemy of compassion, but he was also utterly reliant on the compassion of the women in his life for his survival – a point generally overlooked by his male biographers but well documented by Prideaux. In the case of his sister Elisabeth this care came with strings attached, and the strings were sticky with poison.
Elisabeth used her brother’s connections with the Wagner family to manoeuvre her way into the anti-semitic circles of the German intelligentsia. From there she made contact with Bernhard Forster, a rising star of the far right. Forster, disgusted to the extent with which Jews had infected the body of Germany decided to create Neuva Germania – New Germany – in a remote region of Paraguay he arranged to lease from the government. Elisabeth married him and funded the plan with her dowry. She proved herself a master publicist, promoting the utopian society via the far-right press.
Pure blooded Aryan migrants to Neuva Germania were disappointed to discover that Elisabeth’s promised El Dorado, described in her articles as blessed with fertile soil, a gentle climate and humble and obedient natives was actually an isolated and inhospitable rainforest pulsing with clouds of mosquitoes, alligators in the rivers, snakes in the grass, more snakes coiled around the trees, jaguars roaring outside their tents at night and torrential rains regularly turning their model society into vast, trackless mudslides. All food and other goods had to be purchased through the Forster-Nietzsches, who presided over the debacle from a handsome newly-built mansion filled with servants. Once word of the appalling conditions in the colony reached Germany the funding collapsed. Forster suffered a nervous breakdown. He poisoned himself in a hotel room in San Bernardino.
Elisabeth returned to Germany. Her poor mad brother needed her! Nietzsche never had a publicist prior to his breakdown. He had one now: he just didn’t know it. Elisabeth demanded his letters back from all his correspondents and asserted legal ownership of them. She prevented publication of his autobiography Ecce Homo because she disagreed with most of the content, instead assembling a jumble of his unpublished notes into a book called The Will to Power, carefully edited and marketed to present him as a prophet of Elisabeth’s brand of militaristic nationalistic anti-semitism. She published highly dubious Nietzsche biographies and established the Nietzsche Archive, where she exhibited the ageing philosopher – now completely non-verbal, dressed up in a white linen shift, like an ancient prophet – to dinner guests.
Elisabeth outlived her brother by 35 years. She was nominated for the Nobel Prize for Literature three times. During World War I she convinced the government to issue Thus Spake Zarathustra to German troops, along with Faust and the New Testament. She befriended Hitler, gifting him Nietzsche’s favourite walking stick, and staffed the archive with Nazis. The notions of a racial superman whose actions are “beyond good and evil” and driven by a will to power became core doctrines of the Third Reich.
Prideaux ends her book on the balcony of the Nietzsche Archive. “I know my fate,” Nietzsche wrote. “One day there will be associated with my name the record of something frightful – of a crisis like no other before on earth, of the profoundest collision of conscience, of a decision evoked against everything that until then had been believed in, demanded, sanctified. I am not a man, I am dynamite.” The vista from the balcony where he once sat in his white shift, looking out over Munich: the streets and trees and fields and villas ends with the smoke-blackened crematoria chimney of the Buchenwald concentration camp.
I Am Dynamite!: A Life of Nietzsche by Sue Prideaux (Faber, $60) is available at Unity Books.